Intro Recommender Systems
Definition: make product/service recommendations to people. Recommender systems want to identify items that are more relevant, so people consume more
- omnipresent in every big online store, streaming platform
- Amazon Example: “Customers who liked this, also liked….”
In Practice:
- large systems
- difficult to build
- expensive to maintain
Key problems:
- need to be fast
- process huge amount of data
- “good” recommendations
Basic functionality
What data do we have?
- Product Data → Category, Features, Meta Data, User ratings, product statistics (How often, correlation with other products, …)
- User Data → (more inconsistent, maybe anonymous) usage information over time, user profile, credit score
Types:
- user-item recommendation (focused on user information, streaming platforms using this primarily)
- item-item recommendation
- content based recommendation (focused on previous visited product, primarily used by amazon)
- collaborative filtering
→ most real systems are hybrids!
Content based recommendations between not-related items? E.g. movie ↔ underwear?
→ difficult problem, mostly unsolved
→ content based recommender systems are mostly by products within the same category, or in hybrid systems
Collaborative Filtering
Implicit Modeling:
- No explicit user model
- No explicit item model
→ instead, use global measure induced by the “context”
→ we give users and items IDs
→ which context do we have
Context:
- usually a simple “quality measure” for the itemsE.g. Ratings (e.g. average #stars), views, sales, likes
Advantages:
- no information about items needed→ easy to add / remove items
- no information on users needed→ works on every user
- Content measure is rather cheap to collect
Basic Functionality:
given: m x n – Matrix, with r(ij)= content measure
n = User IDs
m = Products IDs
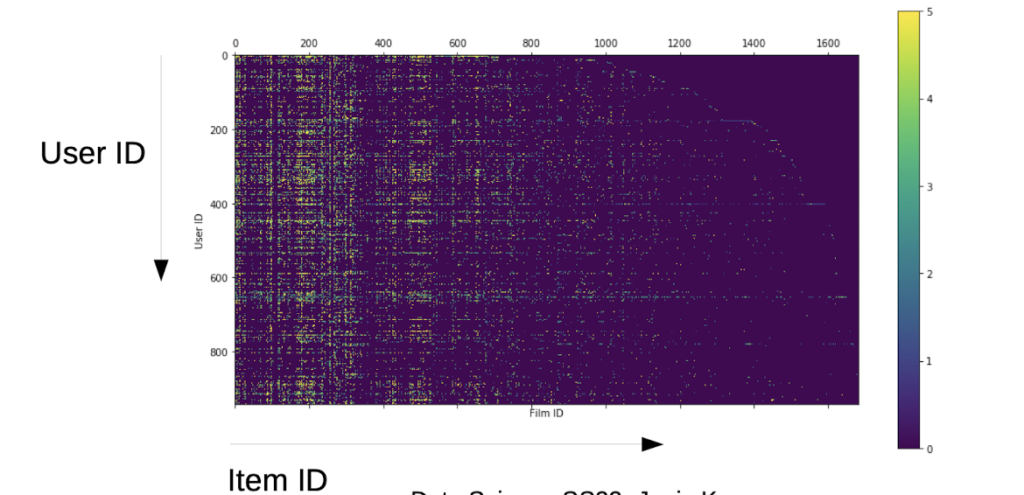
How to find similar items?
= how to measure the distance between items in R?
Items are encoded in column vectors, distance between vectors show how similar the items are (little distance → similar items)
→ Euclidean, Manhattan or Cosine distance
→ practice has shown that cosine distance is good
→ gives relation between items, not the absolute distance
How does Cosine distance work?
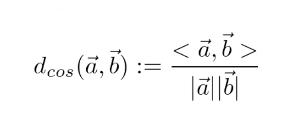
→ if we calculate all distances, we get a square matrix
(we only need to calculate half of the Matrix, because the other side is symmetric)
Note: If we wanted to make a user-to-user matrix (similarities between users), cosine distance is not the best. Pearson’s Correlation is better.
Scaleability Problem:
e.g. amazon has ~300 million products and an extremly large user table
→ huge matrix
→ with almost only zeros, because users hardly see/review any of those products
Standard solution: Singular Value Decomposition
Tensor Algebra
- What is a tensor
- basic vector/matrix algebra
- eigen values-problems and applications
- singular value decomposition (SVD)
- …
Operations for Recommender Systems
We can store vectors in vector spaces
→ most common is the eucledian basis (two vectors e(x), e(y))
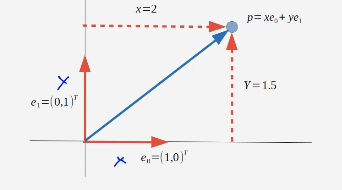
→ but every set of vectors is possible with we can project every other possible vector with a linear combination
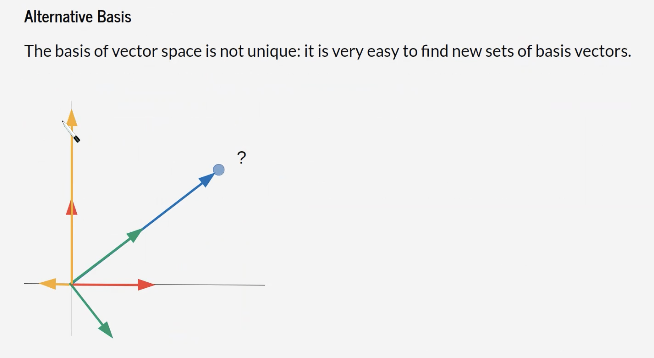
Optional Properties:
- orthogonal
- orthonormal (length = 1)
Eigen Decomposition
→ we search for the best possible vector space for our given data
→ Decomposition in Eigen Values (importance of basis vectors) and Eigen Vectors (new Basis)
Changing the Basis of a Vector space
→ we step aside and look how the basis projects itself
Linear Transformation:



→ We can eliminate the vectors with value 0
even vectors who are near 0 (with compression losses)
What if we don’t have a square matrix (e.g. amount of users ≠ films)
→ Single Value Decomposition (general, works with every matrix)
Code Exercises
(Links to Github)