
Hi, I'm Adrian
I occasionally post about anything I do. This blog is just a reflection of my personal experiences, and I use it to clear my thoughts. If you have some corrections or additions, feel free to contact me!
Enjoy,
Adrian
Adrian
Latest Projects
View all →

Quantum Materials Hackathon - Superconductivity - CERN / ETH
Background During my time as a summer research student at CERN in Geneva, I participated in a Qu...
July 2025
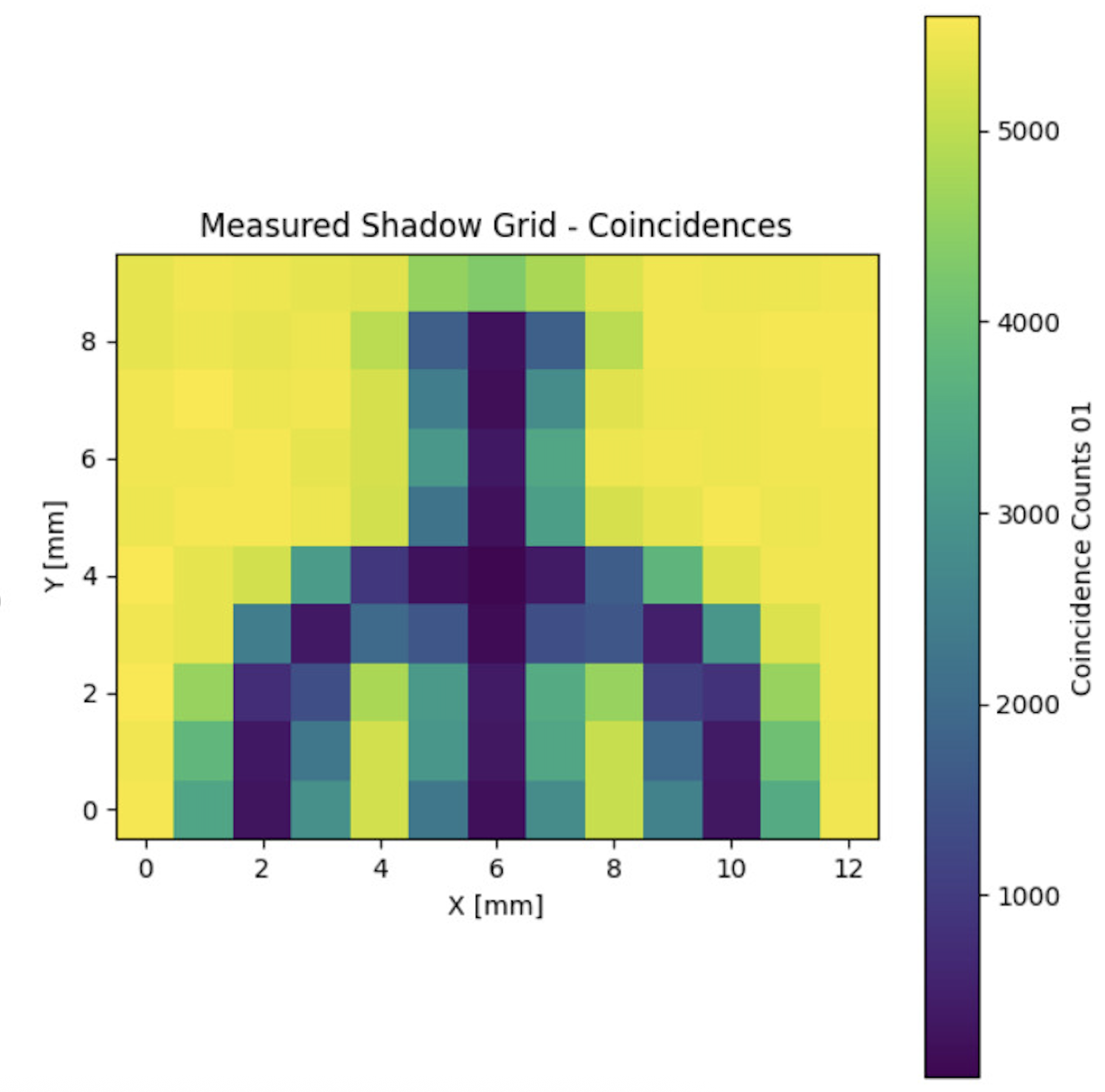
Quantum Ghost Imaging: Creating Images Through Quantum Correlations
What Is Ghost Imaging? Quantum ghost imaging is a counterintuitive technique that uses spatially...
May 2025
Latest Writing
View all →