Bitcoin Wallets

Wallets are applications which serves as a user interface. They control access to the bitcoin, managing keys and creating/signing transactions.

Technically, the word “wallet” refers to the data structure used to store and manage a user’s keys.

Overview

Wallets don’t store bitcoin, just the keys. The coins are recorded in the blockchain. Therefore, a bitcoin wallet is actually a keychain. There are two primary types of wallets, distinguished by whether the keys they contain are related to each other or not.

A nondeterministic wallet contains keys which are not related to each other. It’s not recommended to use this type of wallet, because it’s hard to manage, back up or transfer keys.

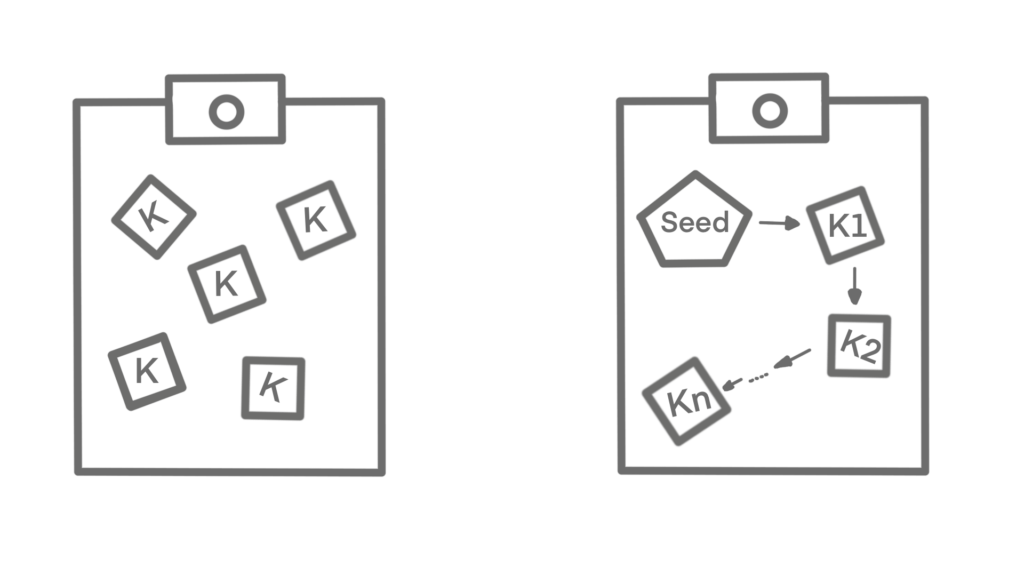
The second type is a deterministic wallet, where all the keys are derived from a single master key, known as the seed. Different key derivation can be used, the most applied derivation method uses a tree-like structure and is known as a hierarchical deterministic or HD wallet. Deterministic wallets are initialized from a random sequence (entropy), which is encoded as Englisch words (mnemonic code words). Private keys are derived through a one-way hash function. This makes it easy to transfer/recover keys.

HD Wallets (BIP-32/BIP-44)

Hierarchical deterministic (HD) wallets contain keys derived in a tree structure. A parent key can derive a sequence of children keys, each of which can derive a sequence of grandchildren keys, and so on.

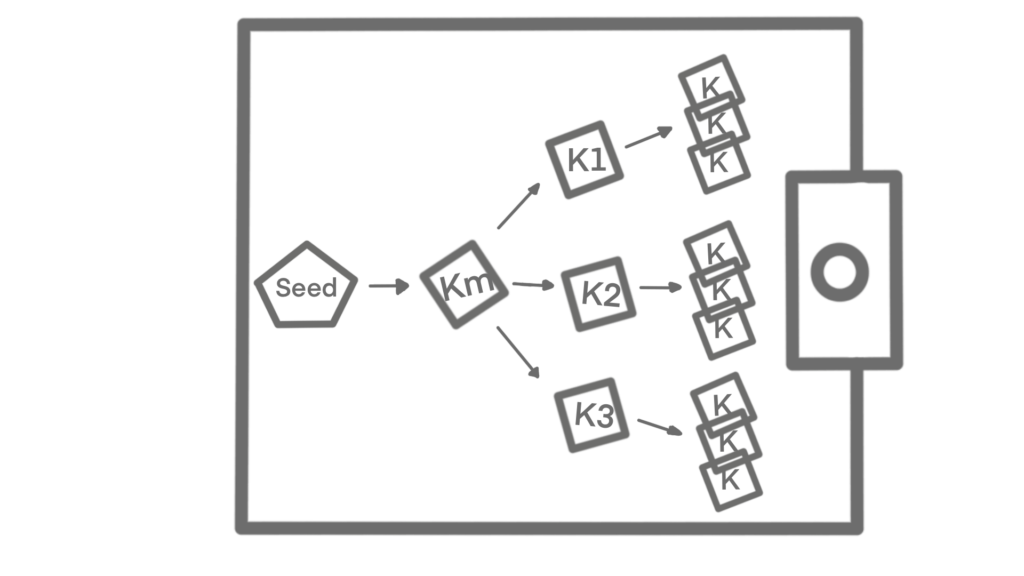
This architecture comes with 2 benefits. Firstly, it provides additional organizational meaning, assign certain branches to speciffic subsidiaries, categories or functions.

HD wallets also provide the opportunity to create a sequence of public keys without having access to the corresponding private key. Therefore, public keys can be created on insecure servers.

Seeds and Mnemonic Codes (BIP-39)

HD wallets are a very powerful mechanism for managing many keys and addresses. It’s even better in combination with a mnemonic seed, which is defined by BIP-39. Note that BIP-39 is one implementation of a mnemonic code standard.

A seed for a deterministic wallet converted from hex in a 12-word mnemonic:

Sidenote: Most hardware wallets generate a more secure, 24-word mnemonic. The mnemonic is used in exactly the same way, regardless of length.

That sequence of words can be used to recover and re-create all the keys in the same or any compatible wallet application.

Generating a mnemonic code

There are 9 steps to create a mnemonic code, defined in BIP-39. The process can be divided into two parts, generating mnemonic words ( Step 1-6) and going from mnemonic to seed (Step 7-9).

Generating mnemonic words:

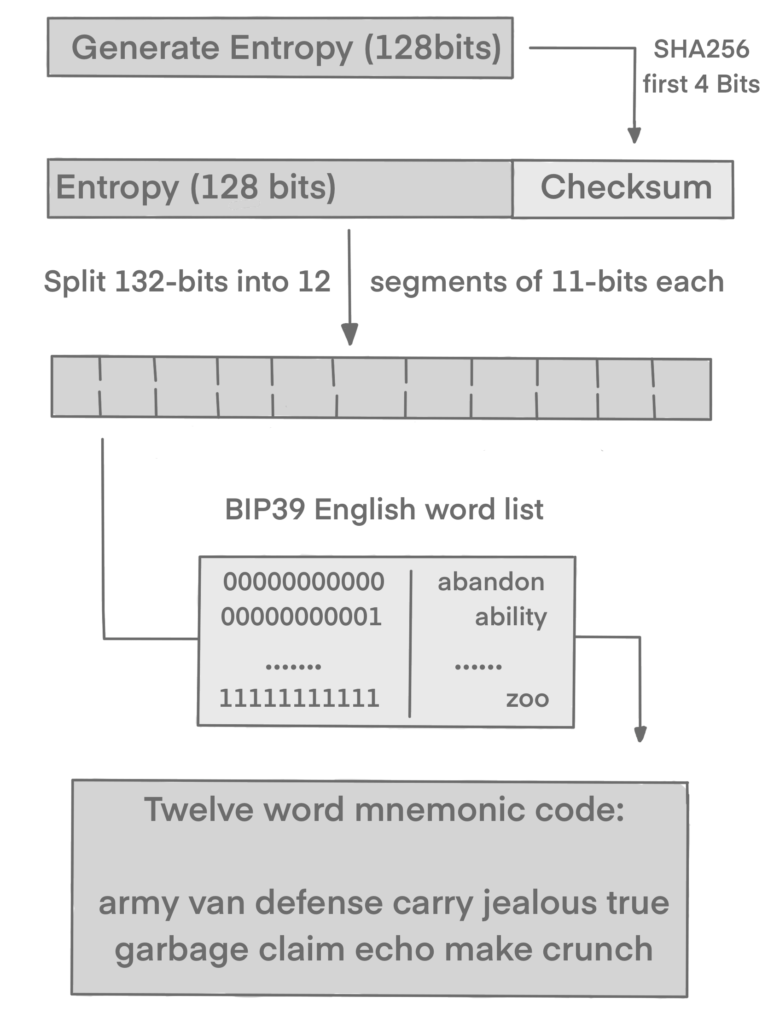
1. Create a random sequence (entropy) of 128 to 256 bits.
2. Create a checksum of the random sequence by taking the first (entropy-length/32) bits of its SHA256 hash.
3. Add the checksum to the end of the random sequence.
4. Split the result into 11-bit length segments.
5. Map each 11-bit value to a word from the predefined dictionary of 2048 words.
6. The mnemonic code is the sequence of words.

Entropy (bits)	Checksum (bits)	Entropy + checksum (bits)	Mnemonic length (words)
128	4	132	12
160	5	165	15
192	6	198	18
224	7	231	21
256	8	264	24

From mnemonic to seed:

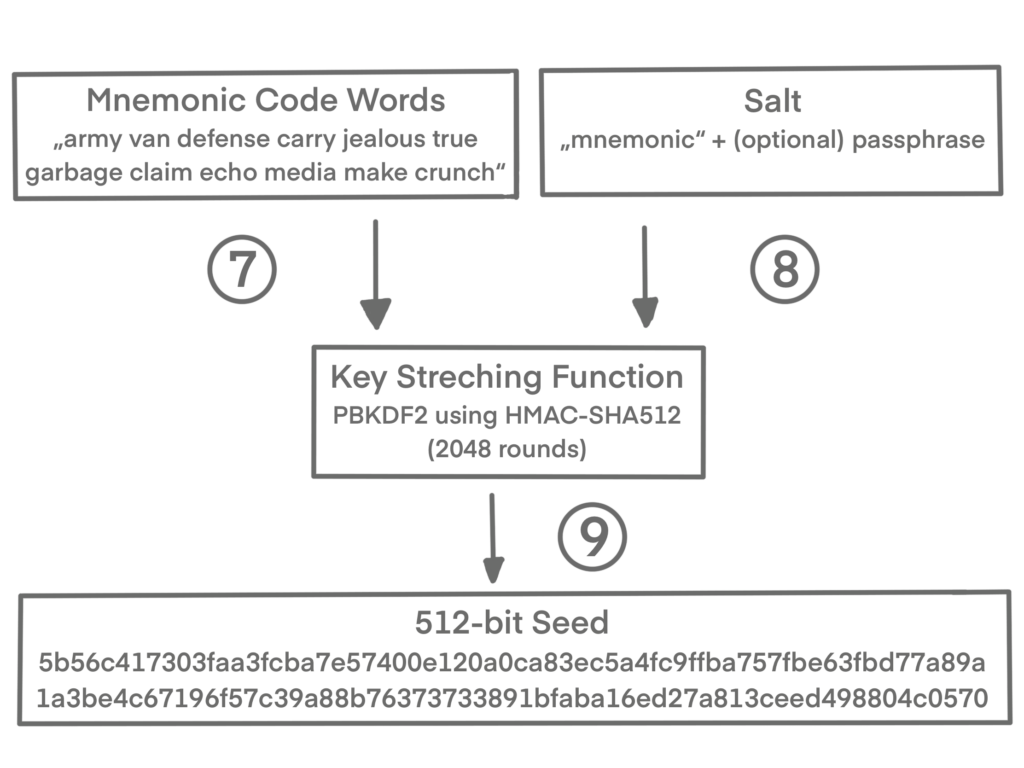
The mnemonic words represent entropy with a length of 128 to 256 bits. The entropy is then used to derive a longer (512-bit) seed through the use of the key-stretching function PBKDF2. The seed produced is then used to build a deterministic wallet and derive its keys.

In order to prevent a brute-force attack, the key-stretching function takes two parameters: the mnemonic and a salt. In the the BIP-39 standard, the salt also allows to include an optional passphrase (as described later).

1. The first parameter to the PBKDF2 key-stretching function is the mnemonic produced from step 6.
2. The second parameter to the PBKDF2 key-stretching function is a salt. The salt is composed of the string constant “mnemonic” concatenated with an optional user-supplied passphrase string.
3. PBKDF2 stretches the mnemonic and salt parameters using 2048 rounds of hashing with the HMAC-SHA512 algorithm, producing a 512-bit value as its final output. That 512-bit value is the seed.

The amount of entropy actually used for the production of HD wallets is roughly 128 bits, which equals 12 words. Any additional entropy is not used for the seed derivation. Therefore, more than 12 words doesn’t lead to more security.

Optional passphrase in BIP-39

In the derivation of the seed, the mnemonic is stretched with a salt consisting of the constant string “mnemonic”. The BIP-39 standard allows the use of an optional passphrase, which is concatenated to the string. This produces a different seed from that same mnemonic.

However, optional passphrases come with two sides. They provide additional security and can even trick an attacker (duress wallet). Besides that, the risks of loosing access to your wallet increases.

From seed to an HD Wallet

Every key in the HD wallet is deterministically derived from a single root seed. Therefore, this seed makes it possible to re-create and transfer the entire wallet easily. 

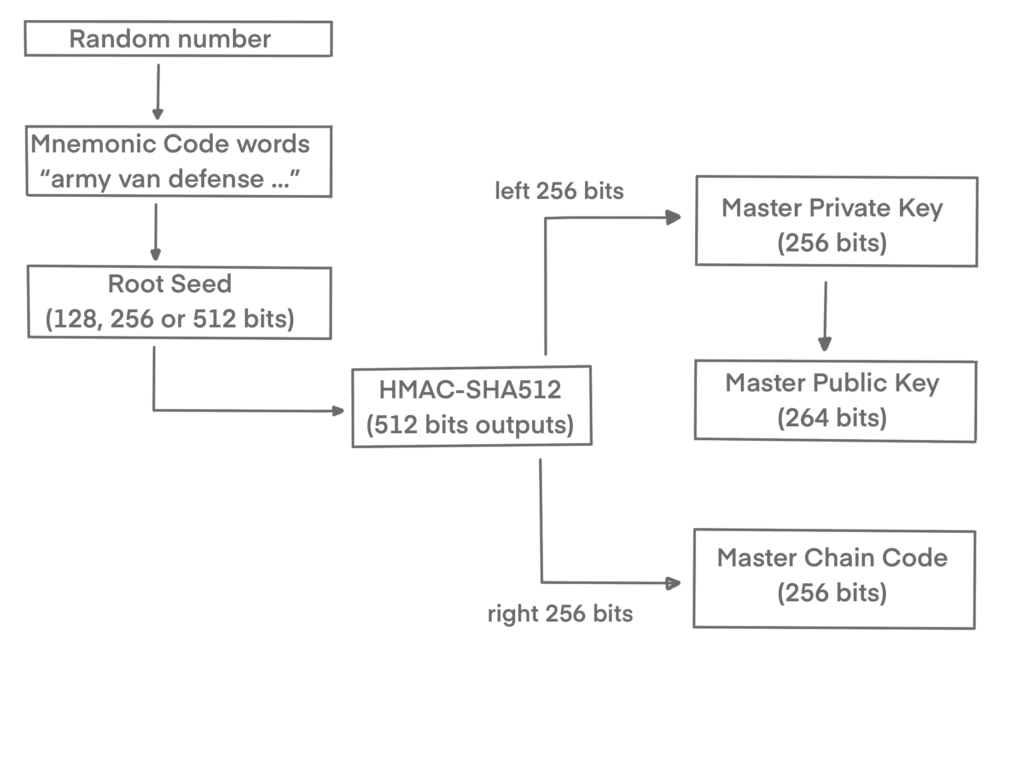
Creating the master keys and master chain code for an HD wallet:

The HMAC-SHA512 algorithm takes the root seed, the resulting hash is used to create a master private key and a master chain code.

The master private key then generates a corresponding master public key using the elliptic curve multiplication, like we learned earlier. The chain code is used to introduce entropy in the function that creates child keys from parent keys.

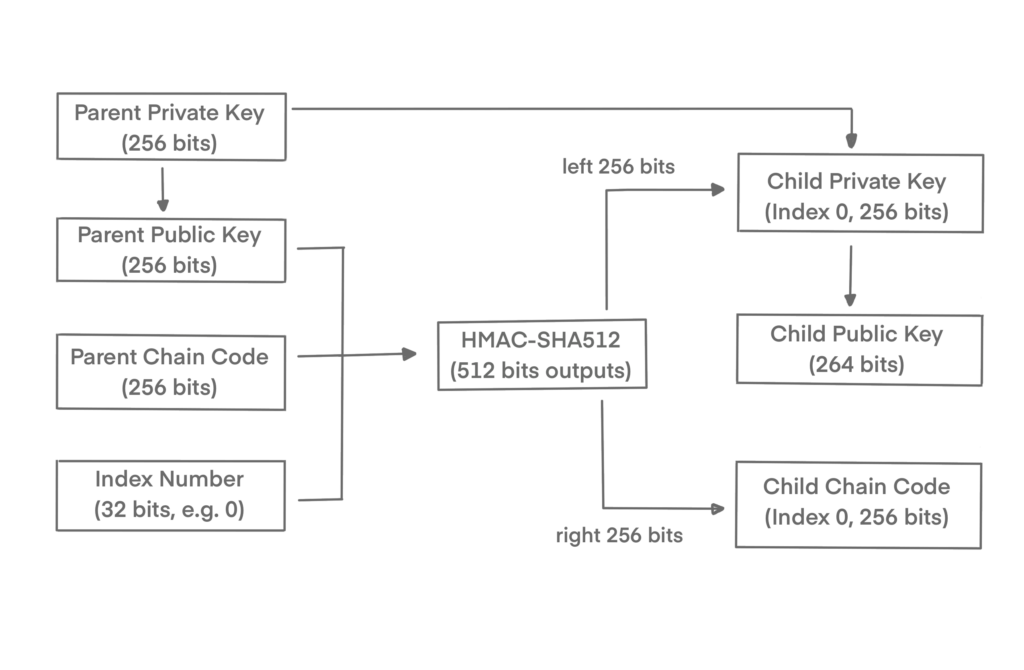
Child key generation:

A child key derivation (CKD) function is used to derive child keys from parent keys.

This is a one-way hash function that combines:

• A parent private or public key (ECDSA compressed key)
• A seed called a chain code (256 bits)
• An index number (32 bits)

The parent private key, chain code, and the index number are combined and hashed with the HMAC-SHA512 algorithm to produce a 512-bit hash, called the extended key. The left half of this hash (256 bits) are added to the parent key to produce a child private key.

Knowing a child key does not make it possible to find its siblings, unless you also have the chain code. The initial chain code seed is made from the seed which is based on the mnemonic.

The extended key can either be private or public. Public extended keys can be unhesitatingly shared with others. In that way, other people can create child public keys for you without knowing the corresponding private key.

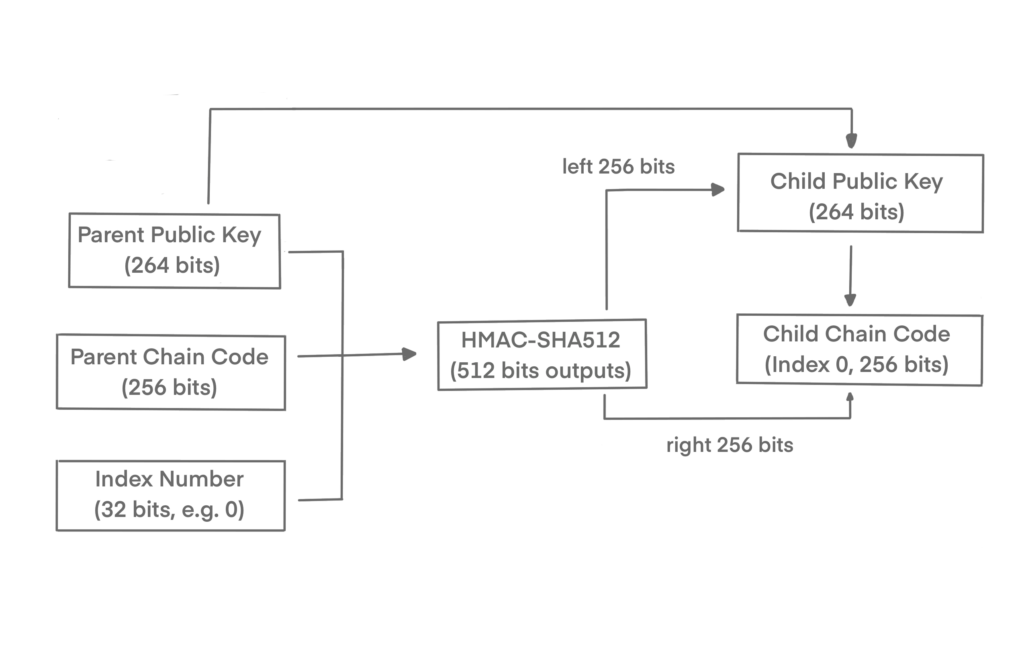
To easily import and export extended keys, they are also encoded using Base58Check. The Base58Check coding for extended keys uses a special version number that results in the prefix “xprv” and “xpub”.

Hardened Derivation

Access to an xpub (which contains the chain code) does not give access to child private keys. But in case a private child key is leaked, it can be used to derive all the other child private keys. Worse, the child private key together with a parent chain code can be used to deduce the parent private key.

To prevent this risk, HD Wallets uses a function called hardened derivation. It takes private key to derive the child chain code which “breaks” the relationship between parent public key and child chain code. Therefore the resulting branch can be used to produce extended public keys.

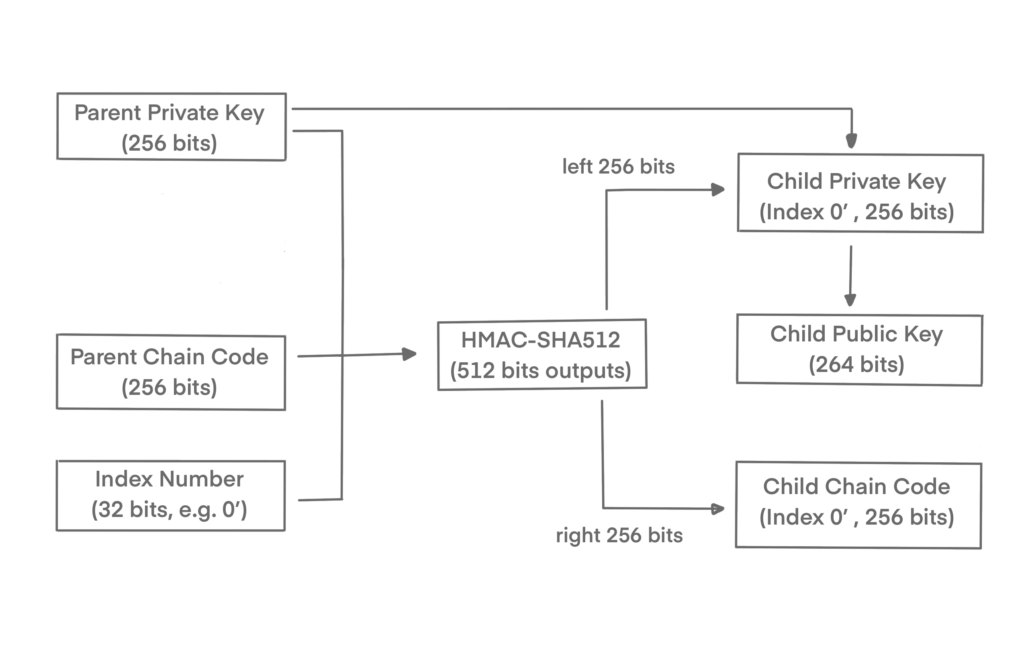
It’s good practice to share public extended keys only when they come from a hardened parent key. Furthermore, the level-1 children of the master keys should be derived through the hardened derivation.

Notes:

• Index numbers between 0 and 2³¹ -1 are used only for normal derivation, 2³¹ to 2³² -1 are used for hardened derivation
• There is a “path” naming convention to identify keys in an HD wallet. Generations are separated with a “/”, it starts with either m (master private key) or M (master public key). 

HD Path	Key described
m/0’/0	The first (0) normal child from the first hardened child (m/0′)
m/1/0	The first (0) child private key from the second child (m/1)

Navigating the HD wallet tree structure

Each parent extended key can have 4 billion children, which offers extreme flexibility. However, it becomes quite difficult to navigate this infinite tree.

BIP-43 offers a solution where the use of the first hardened child index as a special identifier that signifies the “purpose” of the tree structure. An HD wallet should use only one level-1 branch of the tree, the index number identifying the structure and namespace of the rest of the tree by defining its purpose.

Example: an HD wallet using only branch m/i’/ is intended to signify a specific purpose and that purpose is identified by index number “i.”

BIP-44 takes that specification further and proposes a multiaccount structure. Every HD wallet following the BIP-44 structure has 5 predefined tree levels:

m / purpose’ / coin_type’ / account’ / change / address_index

To signalize that we are following the BIP-44 structure, the pupose’ is always set to 44′. The coin_type is designed for multicurrency wallets, where different cryptocurrencies have their own subtree (BTC = 0′).

Account’ allows the user to create logical subtrees for accounting or organizational purposes.

The fourth level “change” is divided into 2 subtrees, one for creating/receiving addresses and one for creating change addresses. To export extended keys, normal derivation is now used. The actual keys used for addresses are in lowest level of the tree.

HD path	Key described
M/44’/0’/0’/0/2	The third receiving public key for the primary bitcoin account
M/44’/0’/3’/1/14	The fifteenth change-address public key for the fourth bitcoin account
m/44’/2’/0’/0/1	The second private key in the Litecoin main account, for signing transactions

Let’s say there is a shop owner with a BIP-44 HD wallet who has provided his extended public key (xpub) to BTCPay Server. A new Address is used for every single transaction, if the payment is cancelled, the bitcoin address is unused and will expire.

At some time, there might be a lot of unused addresses.

BTCPay Server will go back to reuse these addresses to fill the gap in address_index.

But if the shop owner wants to count his money, e.g. with a watch-only wallet (link), when should he stop checking the indexes?

Most wallets follow a predefined limit (gap limit), where the wallet will stop looking for used addresses. The default gap limit is detailed in BIP-44, which is typically 20.

Sidenote: gap limits are often the reason why balances are falsely displayed. Many wallets allow the default gap limit to be changed.