Feature Extraction and Deep Learning

Table Of Contents
  1. Feature Extraction
  2. Feature Engineering
  3. Feature Reduction: PCA
  4. Deep Learning
  5. Training of Neural Networks
  6. Basic Types of Deep Neuronal Network Architectures
  7. Recurrent Neural Networks
  8. Generative Adversarial Neuronal Networks (GAN)
  9. Code Exercises

Feature Extraction

Recall Supervised Classification

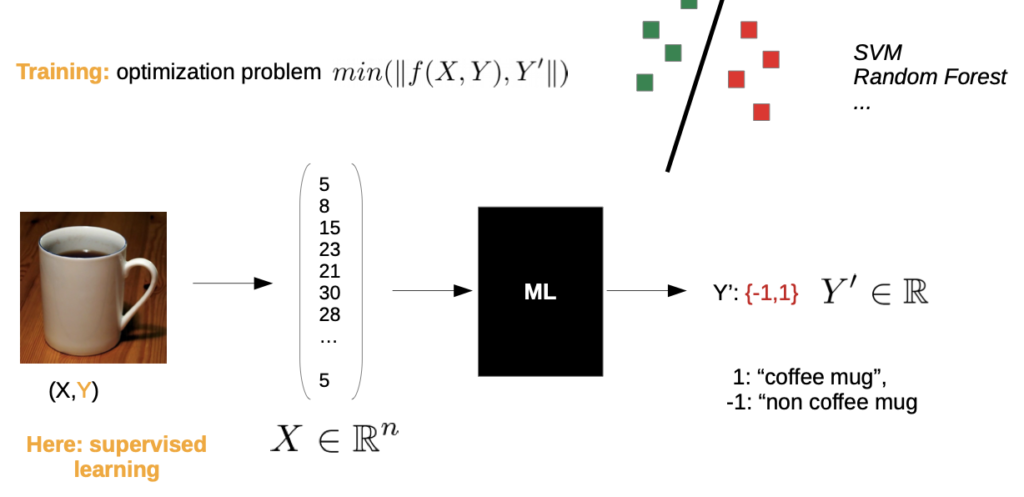
  • the chosen vector space representation aligns the chosen model and how we make a classification
  • earlier, we took pixel by pixel and write it in the vector space

Problem: If we took a slightly other camera angle, there is still a coffee mug, but it’s a whole different point in the space

→ Classification could be wrong

Different solutions:

  • if we have a picture of every possible camera angle , we could evaluate more correctly→ what if the size of the coffee mug differs?
  • feature engineering“preparation”, so our model can evaluate correctly

Feature Engineering

Solution: Shallow Learning

Unstructured data —> Feature Engineering (mathematical operator) —> “mathematical finger print” (feature space)

Properties:

  • preserves information semantic classes have in common, throws away the rest
  • the mathematical finger print doesn’t change much when e.g. the camera angle varies (called invariant or robust)
  • Reduces ****the dimensionality of the problem

Drawbacks:

  • good feature extraction is hard to find (high manual workload)
  • feature extraction is very data specific

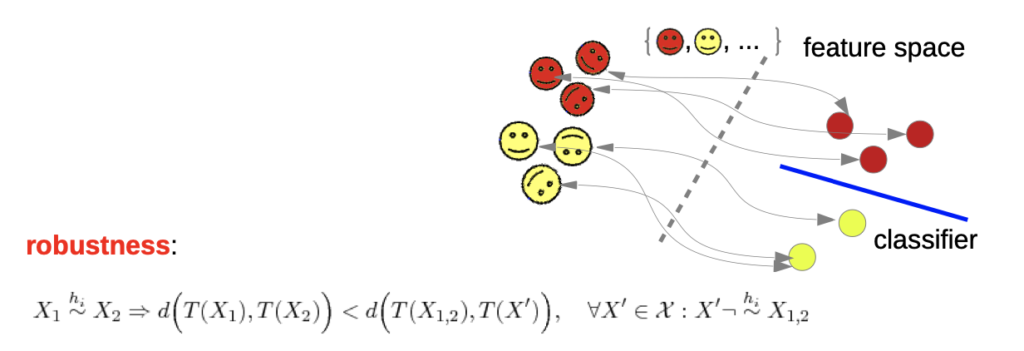
Invariant Theory

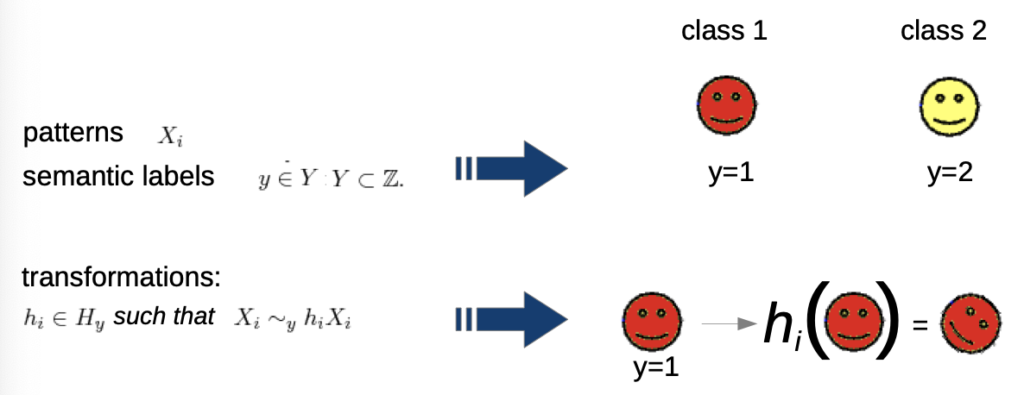
  • transformations can be anything, even don’t have to be mathematically

→ we want to define invariance:

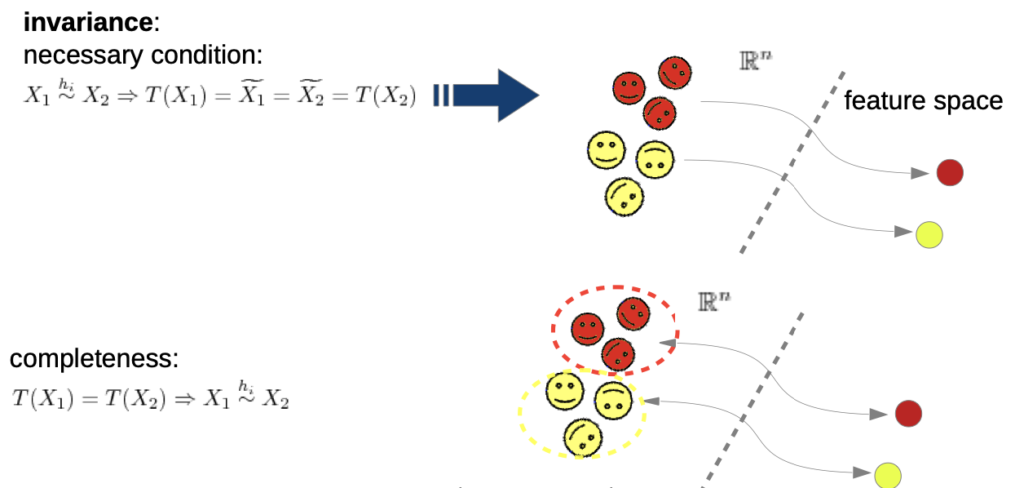
  • given are two data points that are equivalent under transformation
  • feature extraction T
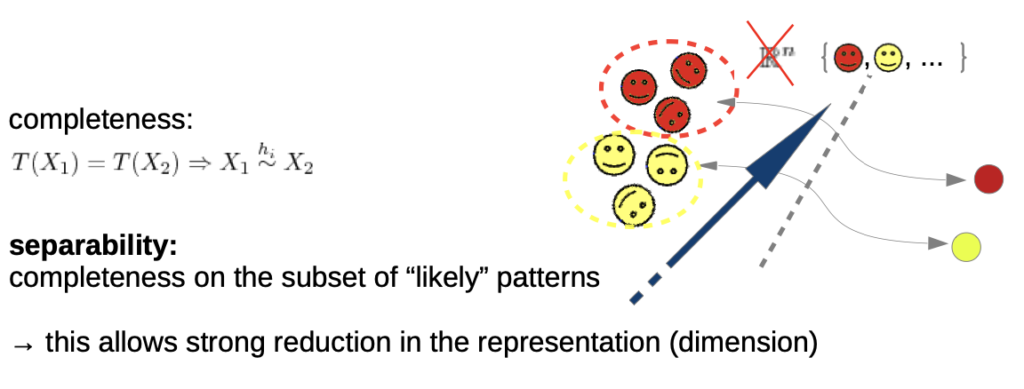
  • we need completeness (transformation backwards), otherwise the trivial solution T(x) = 0 would be valid(we don’t need to know how “much” they were transformed, but which class they are assign

→ in praxis, these is nearly impossible to reach

→ we “weaken” the invariance

separability: we don’t demand invariance for all, but for our training samples

Discussion

Feature extraction vs learning algorithms:

I. if we had perfect features, learning would be trivial II. if we had perfect classifiers, we would not need features

Features are usually used to introduce prior knowledge about the Structure of the data and variances to the learning algorithm**.**

There isn’t the perfect feature, most often you need clustering of different approaches

In practice:

  • Good features are hard to find
  • Often based on complex mathematical functions
  • Depend on the application (domain knowledge needed!)

Generic Approaches:

Invariance by differentiation: set properties into relation / normalization Invaraince by integration: compute average properties

Motivation

  • Very high dimensional representations require a lot of data to fill this huge space (curse of dimensionality)
  • Danger of overfitting is higher if space is only sparsely sampled

→We would like to “compress” our data (with steerable loss) to a lower dimensional representation

**Feature Reduction: PCA Recall:

  • Co-VarianceMatrix (Week3)
  • EigenValueDecomposition (Week2)

Combining both concepts for dimension reduction via Principal Component Analysis (PCA)

Feature Reduction: PCA

PCA Algorithm in a nutshell

  1. Compute Co-Variance Matrix of the data

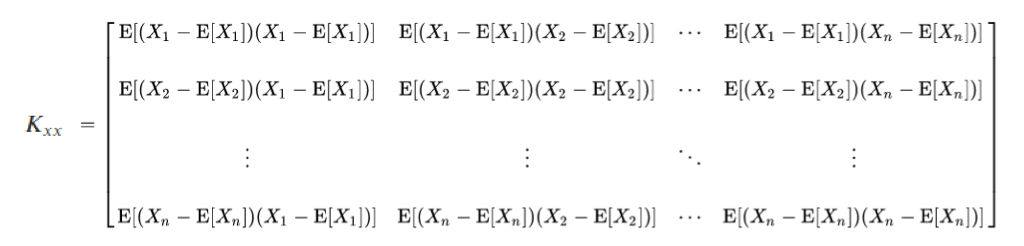
where E[X] is the expected value (mean)

  1. Compute Eigen Vectors and Values of K[xx]
  2. Sort Eigen Values
  3. Select cut-off value
  4. New basis: project to Eigen vectors New dimension: #Eigen values selected

Deep Learning

Intro

  • On an implementational level, deep Learning are very large neuronal networks
  • also called 3. generation of neuronal networks
  • we still are in machine Learning, there still isn’t a strong KI
History

  • Modern architectures have evolved very far from the original perceptron→ in a pure Deep Learning lectures, we would go from left to right, but we focus on the modern models

    • Deep Learning as a blackbox

    • is a subset of ML algorithms
    • our blackbox model is still valid

    What is different?

    Before:

    • most ML algorithms are limited to tight input/output domainse.g. image to vector, always scalar output
    • Pre- and post-processing needed to solve more complex problems!

    Now:

    • capacity of learned mapping is better→ natively allows structured (tensor) in- and output
    • “End to End” learningFeature extraction is difficult, can we make this step learnable? (Shallow Learning)→ but still 2 steps, even if these steps are connected→ “End to End” learning, learn decision space and function in one optimization problem
  • Example: content creation
    • “End to End” learningFeature extraction is difficult, can we make this step learnable? (Shallow Learning)→ but still 2 steps, even if these steps are connected→ “End to End” learning, learn decision space and function in one optimization problem

    Opening the blackbox model

    (brief intro)

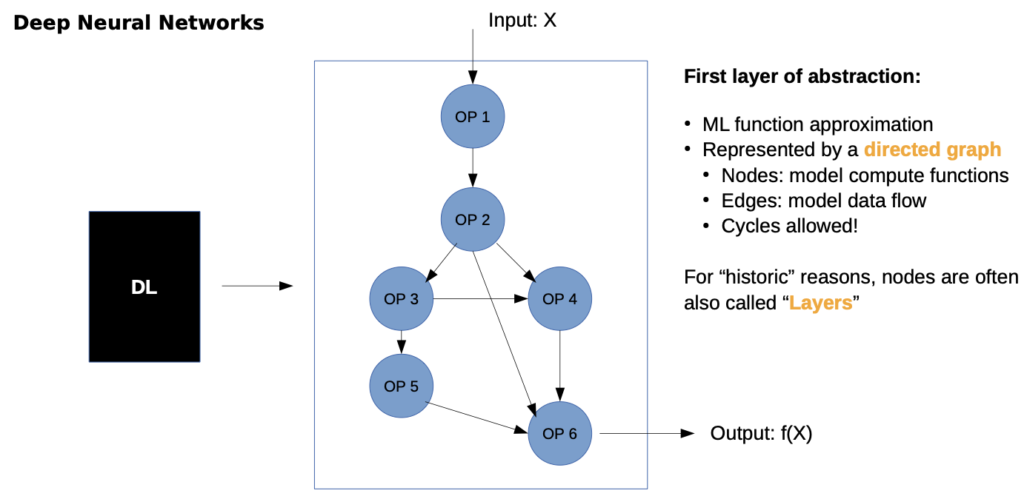
    • we don’t have one big function, rather we partition the problem in other functions
    • Only constraint:partially differentiable (for training)
    • Depending on application and data some have learnable parameters, others are static In- / Output are tensors
    • later we can’t make this easy assignment, because steps are mixed

    Simplest Example of DNN: Multi Layer Perceptron (MLP)

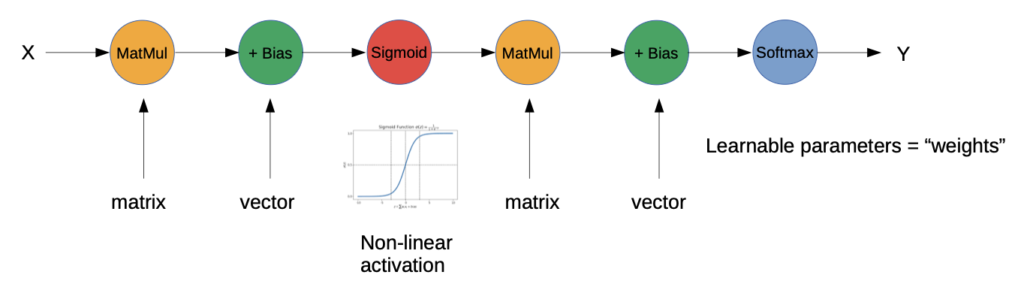
    More complex deep DNN example:

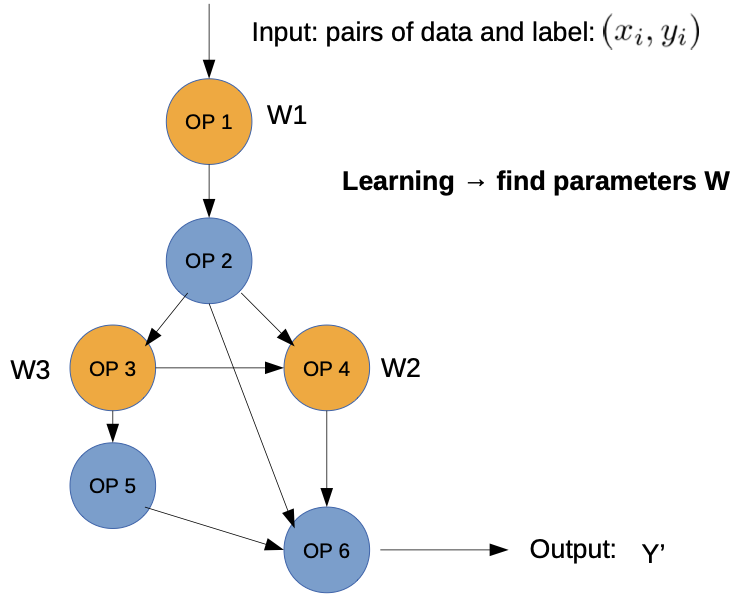
    Training of Neural Networks

    Training of DNNs is an optimization problem: (example for supervised learning)

    1. Run data samples through graph → “forward feed”

    2.Get result y’

    3.Define differentiable “loss function” to measure “difference” between prediction and true label

    4.Optimization objective: minimize loss

    Optimization Problem:

    • J is our Loss function

    Problem: Non CONVEX optimization problem in a very high dimensional space

    → we don’t know if the solution is the best one (could be local minima)

    → NP-HARD PROBLEM

    → numeric and stochastic solution

    How to get the nested gradients?

    → With Back Propagation algorithm

    1. feed forward and compute activation
    2. compute error gradient between true Y and predicted Y’
    1. compute derivative by layer

    → chain rule (we calculate backwards each gradient with the cain rule)

    1. update all weights with small step in gradient direction

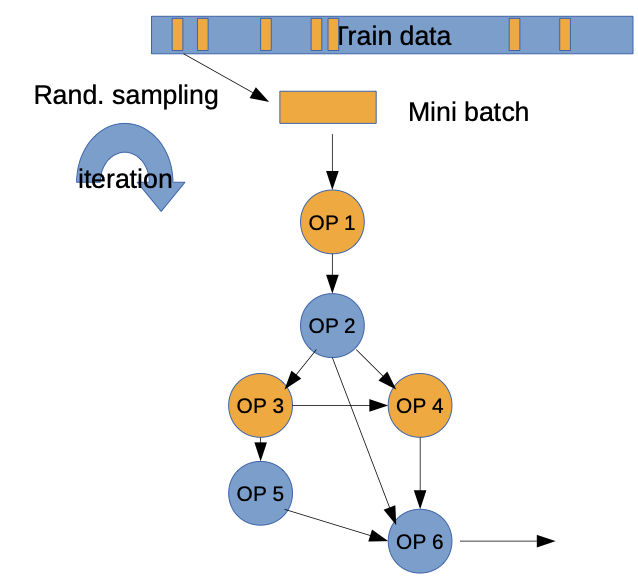
    BUT: Using all of the training data to compute the gradient is computational infeasible

    Instead: Monte Carlo approach: select random batch (small set of training data) per iteration to compute the gradient → SGD

    Stochastic Gradient Descent (SGD)

    we use random to escape from possible local minima and to calculate gradients without running over all data

    → non-smooth convergence

    → many iterations needed (also called epochs)

    → need additional parameters

    • Step size (learning rate)
    • Batch size
    • …

    Pitfalls of DNN training

    1. Optimization Algorithms have many hyper parameters (that have great effect on the outcome)
    2. Optimization is not deterministic (local minima, random initialization)
    3. Optimization is very compute intensive
    4. DNN training is likely to overfit

    → regularization

    1. Needs a lot of training data to learn the underlying distributions
    • not only many data points, also good sampling
    • data annotation (for supervised DL)

    → especially in 3 to 5, progress in hardware and data are the core drivers

    Basic Types of Deep Neuronal Network Architectures

    Basic Architecture of Multi Layer Perceptron (2nd Generation Neuronal Networks):

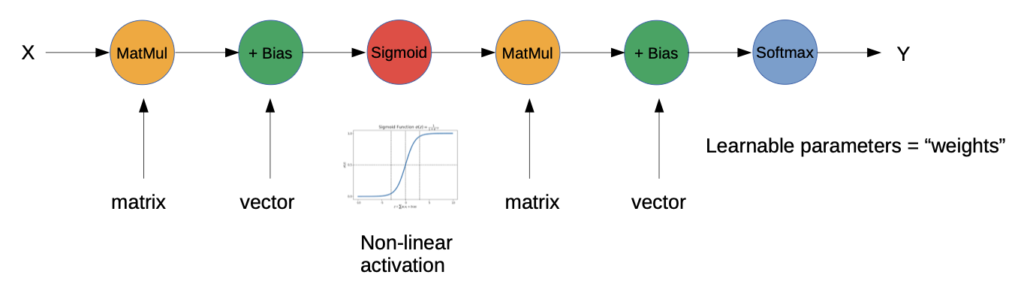
    Where are the Neurons?

    → How do we implement the feature extraction?

    → we have to look at the operators

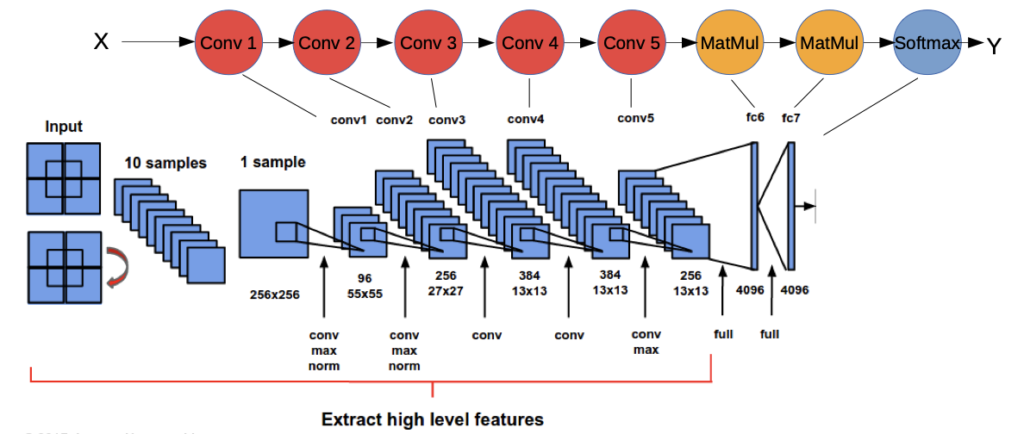
    Convolutional Neuronal Networks (CNN)

    • Most prominent type of DNN (LSTMs are catching up)Responsible for many practical breakthroughs
    • Able to capture locality at multiple scalesWorks well for data with locally embedded structures, e.g. images, videos, audio, graphs … even text
    • Learns Filters which are applied via convolution(End-to-end optimization)

    Typical Design: (AlexNet)

    • New Conv operators

    Exkurs: Convolution

    • is a mathematical operation between two functions

    (here over time series [t])

    (wikipedia example animation here)

    → we have discrete functions, often multi dimensional, e.g. image in 2D

    → we have to adapt

    Convolutional Filters

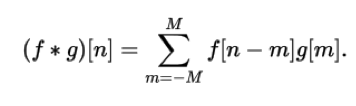
    • f is the image
    • g is the filter
    • image is much large than the filter

    → We “sum of a element wise multiplication over a sliding window”

    • = filter is moved over the image

    Example:

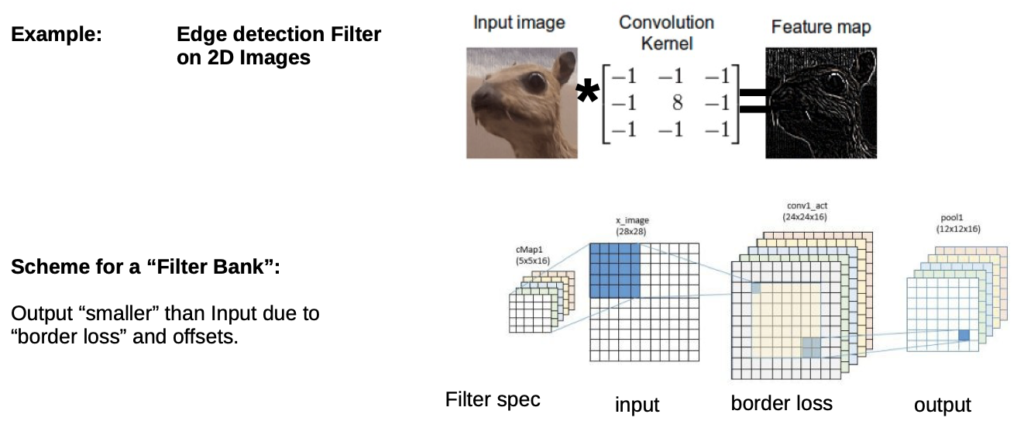
    • we don’t select a filter (Convolution Kernel), we learn which filter fits best for our problem
    • we have a “filter bank”, we choose which fits our problem the best
    • Stride: step size in which we move

    Capturing image statistics of natural scenes

    • at the lowest level, pictures are edges

    Recurrent Neural Networks

    • Networks for sequence learning
    • typical applications: text analysis, translation (sequence to sequence), audio, sensor data→ time series, well logs, …
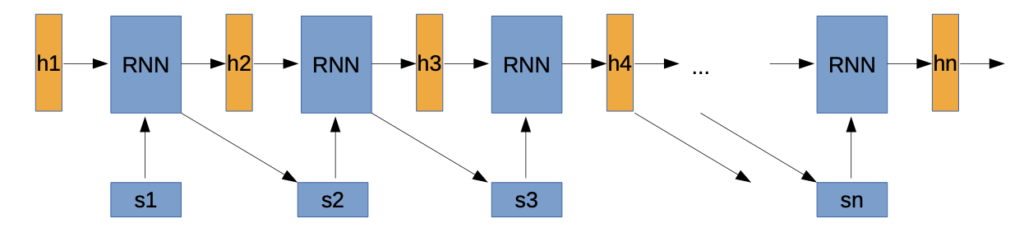
    • s1, s2, … sn are Input sequence
    • h1, h2, … hn are “hidden” vectors, coding the current state in the sequence→ hn can be used, e.g. as input for classification
    • Recurrent DNN, usually LSTM or GRU, but more complex DNN possible
    • RNN predicts next sequence element

    Generative Adversarial Neuronal Networks (GAN)

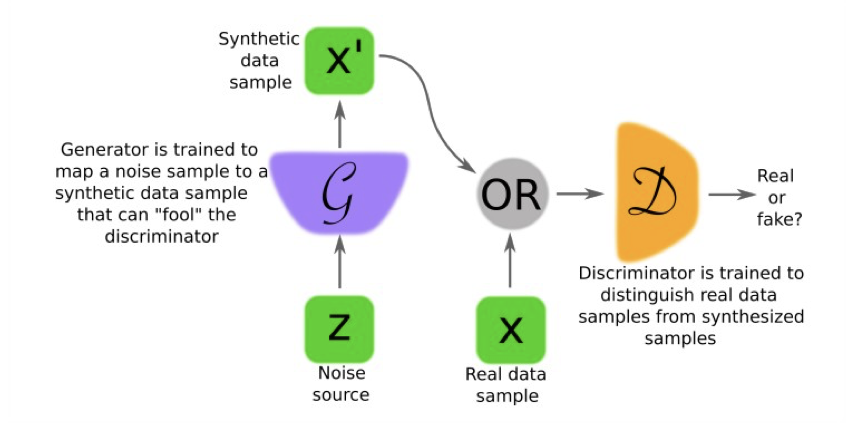
    In a Nutshell, Generative Adversarial Nets are:

    • No classification or Regression, instead we reproduce data (probabilities)
    • Groups of DNNs (at least two)
    • Working against each other→ Generator gets a negative gradient if the Discriminator knows if he image was real or fake
    • Min parts
      • Discriminator Network
      • Generator Network

    Code Exercises

    (Links to Github)

    Intro_to_keras_for_engineers_week7.ipynb

    Week7_CNNs_solution.ipynb