Like I written earlier, Bitcoin is based on cryptography. Cryptography can be used to prove knowledge of a secret without revealing that secret (digital signature), or prove the authenticity of data (digital fingerprint).
This chapter will be about how control ownership of funds, in the form of keys, addresses, and wallets are possible through cryptography.
Overview
Ownership of bitcoin is established through digital keys, bitcoin addresses and digital signatures. The digital keys are not stored in the network, but are instead created and stored by users in a file, called a wallet. The digital signature can only be generated with a secret key.
Keys come in pairs consisting of a private (secret) key and a public key. For a better understanding, the public key is like your bank account, where the private key is your PIN. Both keys are rarely seen by other users, they are mostly stored in the wallet.
For transactions, the recipient’s public key is represented by its digital fingerprint, called a bitcoin address. This address is (mostly) generated and corresponds to the public key.
The mathematics used in Bitcoin
Public key cryptography was invented in the 1970s and is a mathematical foundation for computer and information security.
This led to the discovery of mathemtical functions, like prime number exponentiation, RSA algorithm or elliptic curve multiplication. These functions are asymmetrical, which means they are easy to calculate in one direction, but extremly hard to calculate backwards.
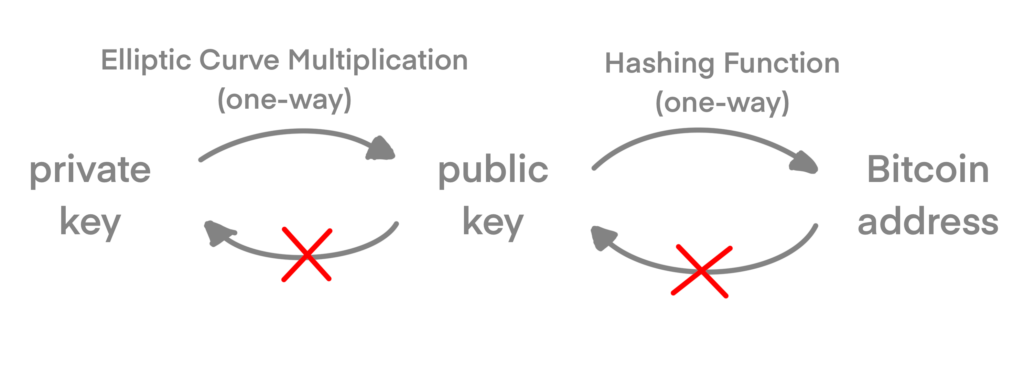
In bitcoin, we use public key cryptography to create a key pair that controls access to bitcoin. The key pair consists of a private key and—derived from it—a unique public key. The public key is used to receive funds, and the private key is used to sign transactions to spend the funds.
When spending Bitcoin, the bitcoin owner presents his public key and a signature (different each time, but created from the same private key) in a transaction to spend those bitcoin. Through the presentation of the public key and signature, everyone in the bitcoin network can verify the ownership and accept the transaction as valid.
Relationship between private and public keys
The private key is a 256-bit number, usually picked random. With elliptic curve multiplication (explained later), we can generate a public key. Now we can create a bitcoin address with a cryptographic hash function.
Generating a private key
Creating a bitcoin key is essentially the same as “Pick a number between 1 and 2256“. The method you use to pick the number does not matter as long as it is not predictable or repeatable.
Here is an example of a private key (in hexadecimal format):
1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD
But what happens if two people pick the same private key?
Technically, if two people pick the same private key, these people can spend each others bitcoin. But the chances are extremely low, because 2256 is an incredibly large number (≈ 1077). To put that into perspective, the visible universe is estimated to contain 1080 atoms. So you need to pick the same atom in the entire visible universe as somebody else has.
Public key:
The public key is calculated from the private key using elliptic curve multiplication:
public K = (private K) * G
G is a constant point called generator point. Calculating backwards, getting the private key, is as difficult as trying all possible values (brute-force search).
Elliptic curve multiplication explained
Elliptic curve cryptography is based on the discrete logarithm problem as expressed by addition and multiplication on the points of an elliptic curve.
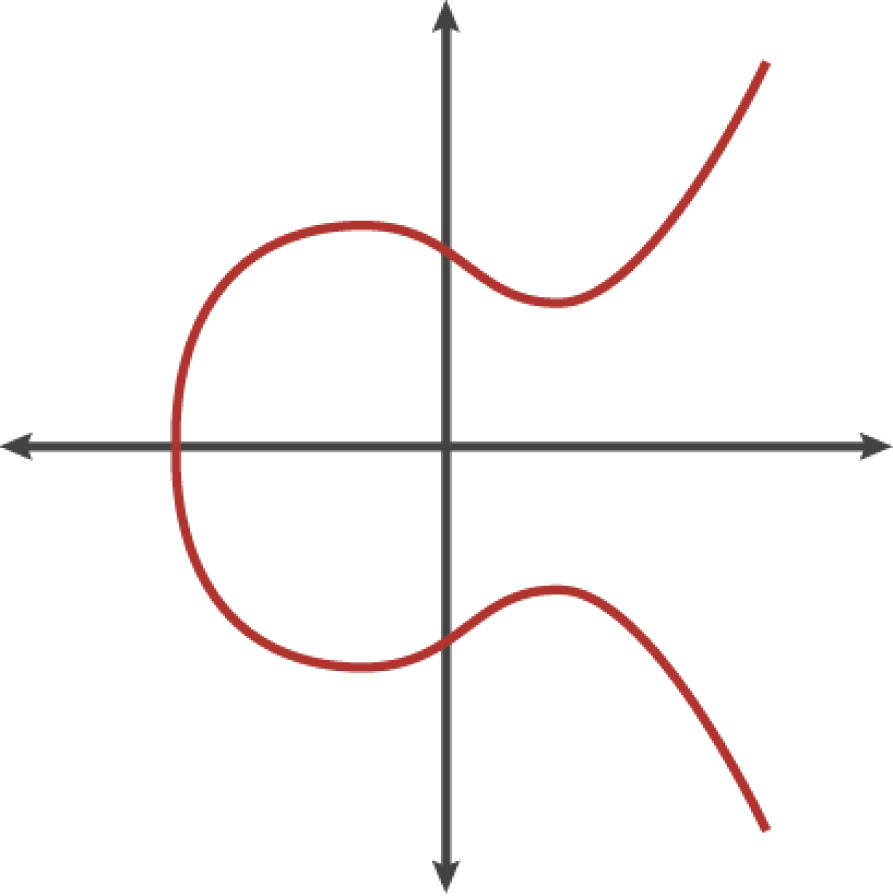
The specific elliptic curve, which is used in Bitcoin, is defined in a standard called secp256k1. It is described by the following function:
y2 = x3 + 7 (defined over the field Zp)
mod p (modulo prime number p) indicates that this curve is over a finite field of prime order p, where
p = 2256 – 232 – 29 – 28 – 27 – 26 – 24 – 1
Because this curve is defined over a finite field of prime order instead of over the real numbers, it looks like a pattern of dots scattered in two dimensions.

So, for example, the following is a point P with coordinates (x,y) that is a point on the secp256k1 curve:
P = (55066263022277343669578718895168534326250603453777594175500187360389116729240, 32670510020758816978083085130507043184471273380659243275938904335757337482424)
Rules for elliptic curves:
- there is a “point at infinity” ≈ the role of zero in common addition, it is sometimes represented by x = y = 0 (which doesn’t satisfy the elliptic curve equation, but it’s an easy separate case that can be checked)
- there is also a “+” operator, where P1 + P2 = P3. If the two points P1 and P2 are on the elliptic curve, then P3 is also on the elliptic curve
- Geometrically, this third point P3 is calculated by drawing a line between P1 and P2. This line will intersect the elliptic curve in exactly one additional place. Call this point P3‘ = (x, y). Then reflect in the x-axis to get P3 = (x, –y).
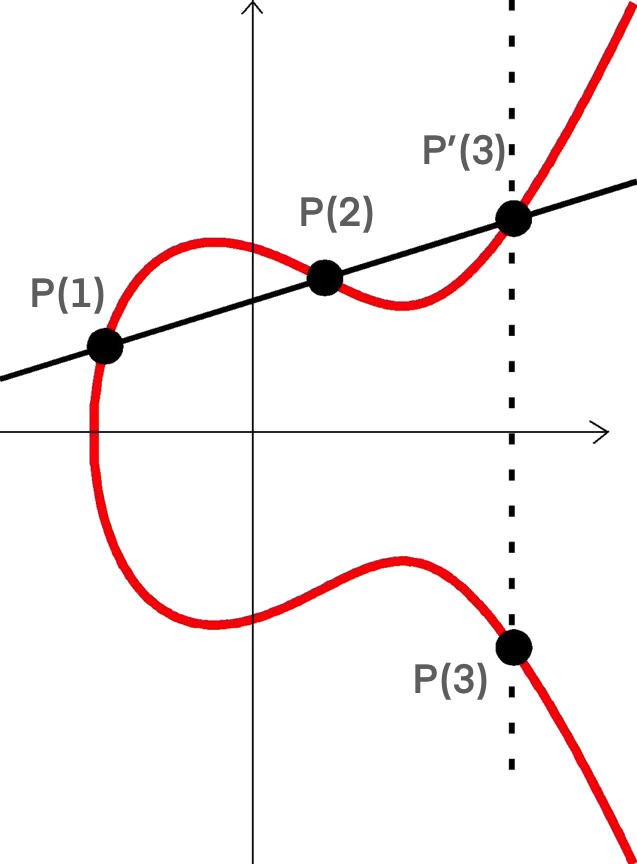
The “point at infinity” has a couple of usecases:
- If P1 is “point at infinity”, then P1 + P2 = P2.
- The addition is also associative, therefore (P1 + P2) + P3 = P1 + (P2 +P3)
- If P1 and P2 are the same point, the line “between” P1 and P2 equals the tangent on this specific point. This tangent will intersect the curve in exactly one new point. You can use techniques from calculus to determine the slope of the tangent line.
- Sometimes (i.e. if P1 and P2 have the same x-values), the line between the points will be vertical. Therefore, P3 = “point at infinty”
Like in common mathematics, there is also multiplication which extends addition in the same way:
P + P + P + … (x times) = x * P
Sidenote: Confusingly, x is sometimes called an “exponent” in this case.
Generating a public key:
We multiply the randomly generated private key with a predetermined point on the elliptic curve with the generator point G. The result is another point on the curve, the public key.
To visualize this process, we think of multiplication like “adding G to itself, (private key) times in a row”. Since addition is nothing other than draw the tanget and finding where it intersects the curve again, then reflecting that point on the x-axis, we just do it multiple times.

Notice that the generator point is always the same. Because there are too many possibilities to calculate it backwards, the private key stays unknown.
Bitcoin Addresses
A bitcoin address starts with the digit “1” and is what appears most commonly in a transaction as the “recipient” of the funds.
Example: 1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy
Like on a paper check, the beneficiary can be flexible. A bitcoin address can represent the owner of a key pair, or it can represent something else, such as a payment script (described later).
Representing the public key, the address is derived from the public key through the use of one-way cryptographic hashing. A hashing algorithm is a one-way function that produces a fingerprint or “hash” of an arbitrary sized input.
These hash functions are used a lot in:
- bitcoin addresses
- script addresses
- Proof-of-work algorithm
The algorithms used to make an address are the Secure Hash Algorithm (SHA) and the RACE Integrity Primitives Evaluation Message Digest (RIPEMD), specifically SHA256 and RIPEMD160.
Generating an Address from a public key:
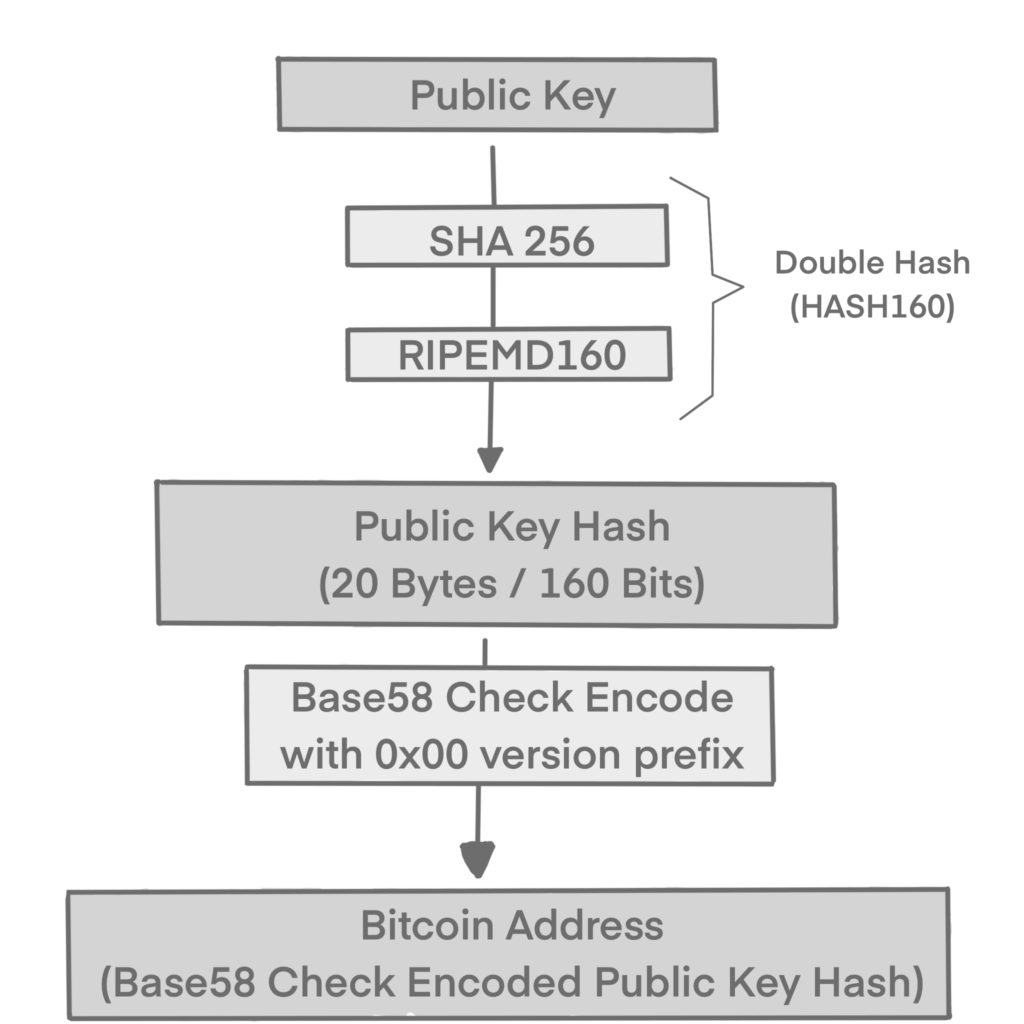
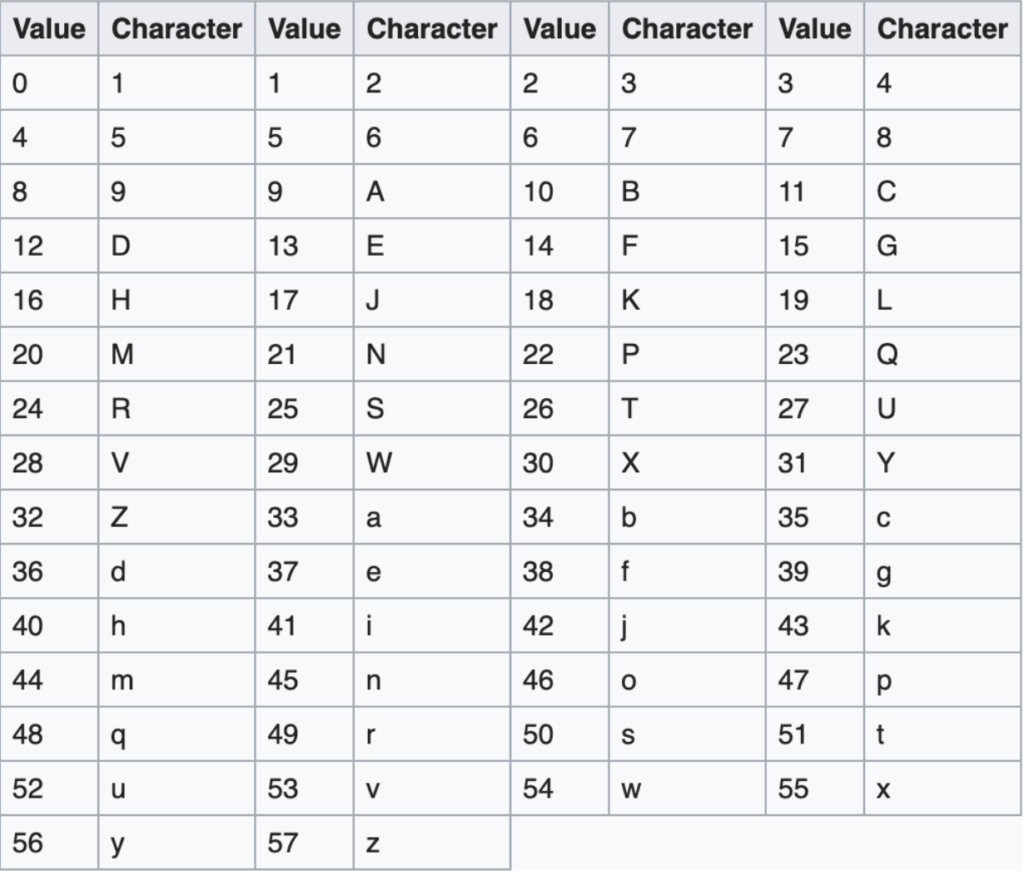
Bitcoin addresses are mostly encoded as Base58Check, which uses 58 characters and a checksum to display large numbers (addresses) more readable and protect against errors.
It is based on the Base64 representation, which is used to to add binary attachments to email. The Base64 alphabet contains 26 lowercase letters, 26 capital letters, 10 numerals (0-9), and 2 special symbols(+; /).
Base58 is a subset of Base64, developed for the use in bitcoin and other cryptocurrencies. It excludes frequently mistaken characters, like 0 (zero) and O (capital o) or l (small L) and I (capital i).
To add extra security against typos or transcription errors, Bitcoin introduced Base58Check. The checksum is an additional four bytes added to the end of the data that is being encoded. The checksum is derived from the hash of the encoded data and can therefore be used to detect and prevent transcription and typing errors. When presented with Base58Check code, the decoding software will calculate the checksum of the data and compare it to the checksum included in the code. If the two do not match, an error has been introduced and the Base58Check data is invalid. This prevents a mistyped bitcoin address from being accepted by the wallet software as a valid destination.
Convert data into a Base58Check format
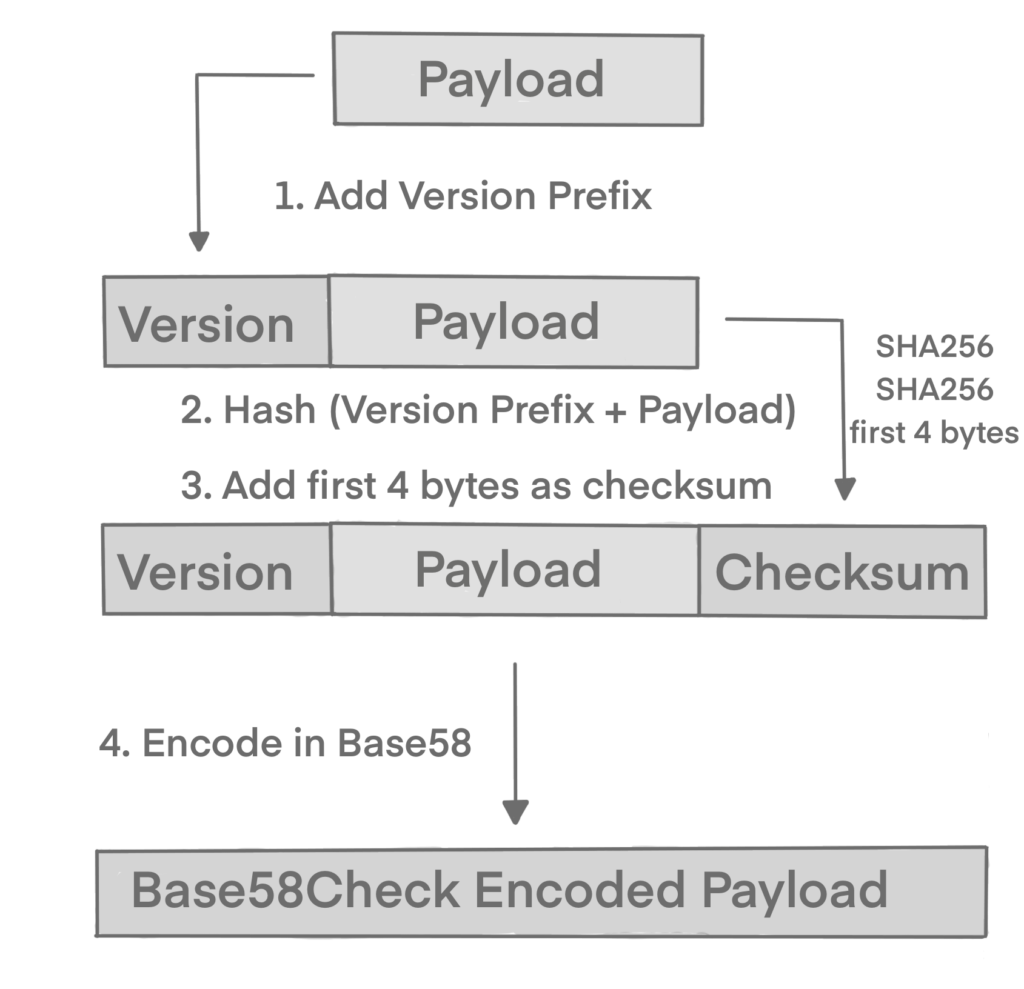
Firstly, we add prefix to the data, called the version byte. This helps to identify the type of data that is encoded. For example, in the case of a bitcoin address the prefix is zero (0x00 in hex), whereas the prefix used when encoding a private key is 128 (0x80 in hex). Watch the table below for further examples.
Next, we compute the “double-SHA” checksum, meaning we apply the SHA256 hash-algorithm twice on the previous result. From the resulting 32-byte hash (hash-of-a-hash), we take only the first four bytes. These four bytes serve as the error-checking code, or checksum. The checksum is concatenated (appended) to the end.
The result is encoded using the Base58 alphabet as described previously.
Now it’s easy for humans to identify the type of data that is encoded and how to use it.
| Type | Version prefix (hex) | Base68 result prefix |
|---|---|---|
| Bitcoin Address | 0x00 | 1 |
| Pay-to-Script-Hash Address | 0x05 | 3 |
| Bitcoin Testnet Address | 0x6F | m or n |
| Private Key WIF | 0x80 | 5, K, or L |
| BIP-38 Encrypted Private Key | 0x0142 | 6P |
| BIP-32 Extended Public Key | 0x0488B21E | xpub |
Private key formats
The private key can be represented in a number of different formats, all of which correspond to the same 256-bit number. For example, hexadecimal and raw binary formats are used internally in software and rarely shown to users. The WIF (wallet import format) is used for import/export of keys between wallets and often used in QR code representations of private keys.
| Type | Prefix | Description |
|---|---|---|
| Raw | None | 32 bytes |
| Hex | None | 64 hexadecimal digits |
| WIF | 5 | Base58Check encoding: Base58 with version prefix of 0x80 and 4-byte checksum |
| WIF-compressed | K or L | As above, with added suffix 0x01 before encoding |
| Format | Private key |
|---|---|
| Hex | 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aedd |
| WIF | 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn |
| WIF-compressed | KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJ |
Since any raw binary encoding for display here would, by definition, not be raw binary data, it is not shown in the examples.
Any format can be easily converted into any other format.
Public key formats:
Public keys can be represented either compressed or uncompressed. Since the public key is a point of the elliptic curve, it is usually represented with the prefix 04 followed by two 256-bit numbers (x,y). The prefix 04 is used to set apart uncompressed public keys from compressed public keys that begin with a 02 or a 03.
Compressed public keys were introduced to bitcoin to reduce the size of transactions and conserve disk space on nodes that store the bitcoin blockchain database. As we saw earlier, the elliptic curve expresses a mathematical function. Therefore we can calculate a point with only the x coordinate by solving the equation:
y2 = x3 + 7 (defined over the field Zp)
That allows us to store only the x coordinate of the public key point, omitting the y coordinate and reducing the size of the key and the space required to store it by 256 bits.
But why are there two prefixes (02, 03) for compressed public keys?
Because of the left side of the equation (y2), there are 2 possible solutions for y. Specifically, there is one solution above and one solution below the x-axis. So we need to store the sign of the y coordinate as well. When calculating the elliptic curve in binary arithmetic on the finite field of prime order p, the y coordinate is either even (prefix 02) or odd (prefix 03), which corresponds to the positive/negative sign.
example: K = 03F028892BAD7ED57D2FB57BF33081D5CFCF6F9ED3D3D7F159C2E2FFF579DC341A
Pay attention to the bitcoin address if you run the double-hash function. The compressed public key produce a different address than the uncompressed. However, the private key is identical for both. Compressed public keys are gradually becoming the default across bitcoin clients. But now, newer clients have to account for transactions from older clients that do not support compressed public keys.
Which addresses should the bitcoin wallet scan for if keys are imported?
Compressed private keys
When private keys are exported, the WIF is implemented differently if compressed public keys were used. This allows the importing wallet to distinguish between private keys originating from older or newer wallets.
Ironically, compressed private keys are one byte longer than uncompressed private keys. This added one-byte suffix just tells the wallet “private key from which only uncompressed public keys should be derived”.
Therefore, we call it WIF-compressed or simply WIF, instead of “compressed private keys”.
| Format | Private key |
|---|---|
| Hex | 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD |
| WIF | 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn |
| Hex-compressed | 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD01 |
| WIF-compressed | KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJ |
While the Base58Check version prefix (0x80) for both WIF and WIF-compressed formats is the same, the addition causes the first character of the Base58 encoding to change from a 5 to either a K or L. It’s like going from 99 to 100, where the number of digits increases by one byte.
Pay-to-Script Hash (P2SH) and Multisig Addresses
Mostly, Bitcoin addresses start with “1”. Addresses that begin with the number “3” are pay-to-script hash (P2SH) addresses, sometimes erroneously called multisignature or multisig addresses. They provide the opportunity to add functionality to the address itself. A P2SH address is created from a transaction script, which defines who can spend a transaction output. Encoding a P2SH address involves the same double-hash function as used during creation of a bitcoin address, only applied on the script instead of the public key.
The most common implementation of the P2SH function is the multi-signature address script. As the name implies, the underlying script requires a minimum number of signatures to prove ownership and therefore spend funds. It’s known as M-of-N multisig, which means you need M signatures from N keys. M is equal or less than N.
These addresses can be used to add security and/or to manage a shared account.
Sidenote: P2SH is not necessarily the same as a multisignature standard transaction. A P2SH address mostly represents a multi-signature script, but it might also represent a script encoding other types of transactions.