Quantum Materials Hackathon - Superconductivity - CERN / ETH

Background
During my time as a summer research student at CERN in Geneva, I participated in a Quantum Materials Hackathon. It was a joint event between CERN and the ETH Zürich. Many organizations like AWS, Fraunhofer, Alice&Bob and SGInnovate were sponsors of this event and gave interesting talks.


Our team at the end of a long, semi-productive work session in front of the Science Gateway (right) and presentation of our solution (left)
Challenge
Initially, we were given a one-pager about the problem we should tackle. It outlined the limitations of classical solutions for discovering new conductors. Even modern GNN-diffusion generators struggle to capture both phase stability and high conductivity. Our task was to implement a quantum-enhanced algorithm that could tackle this problem.
While the one-pager focused on superconductivity, we were free to choose any material or alloy and just improve its conductivity. The challenge also included some non-technical tasks related to economics, impact and ethics. That part was mainly done by other team members, so I won’t go into detail here, but they can be found on the GitHub page.
Material Selection
We decided to focus on copper alloys. There was a great graphic showing the trade-off between hardness and conductivity in those alloys, and we wanted to explore this area. We chose to simulate graphene-copper alloys, mainly because of all the promising experiments recently done with graphene, especially related to its unique properties regarding conductivity and hardness.
Our Solution
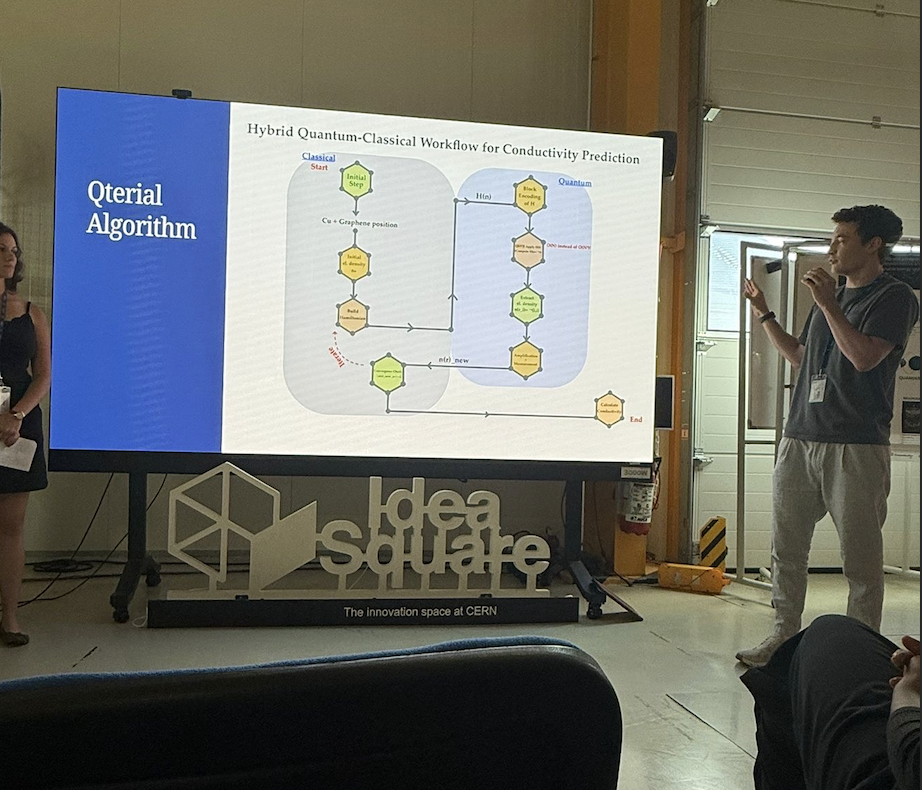
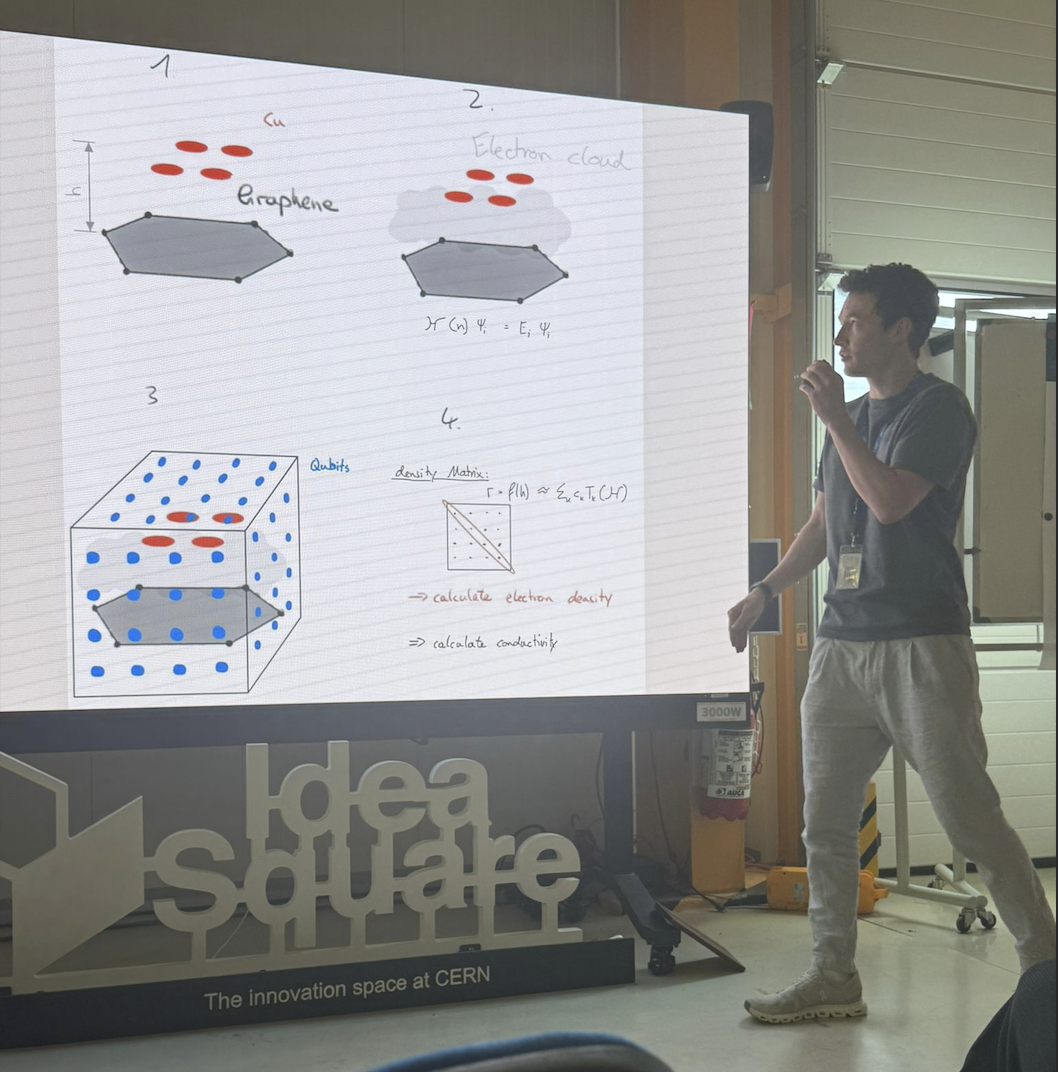
Final Presentation of our Solution
Our solution was heavily inspired by this paper on quantum-accelerated density functional theory (DFT) using Quantum Singular Value Transformation (QSVT). The core idea was to create a hybrid quantum-classical workflow for predicting material conductivity.
The Technical Approach
We implemented a quantum-enhanced self-consistent field (SCF) method that works roughly like this:
-
Classical Setup: Start with the molecular geometry of our copper-graphene composite and build the initial Hamiltonian matrix describing the electronic structure.
-
Quantum Processing: Use QSVT to approximate the Fermi-Dirac function, which tells us how electrons are distributed at different energy levels. This is the quantum “magic” - instead of diagonalizing huge matrices classically (which scales cubically with system size), we use quantum circuits that scale much better.
-
Density Extraction: Extract electron density information from the quantum circuit using amplitude amplification techniques.
-
Self-Consistency Loop: Feed this density back into the Hamiltonian and repeat until convergence. This gives us the ground state electronic structure.
-
Conductivity Calculation: From the final electronic structure, we calculate the density of states at the Fermi level, which directly relates to electrical conductivity.
The beauty of this approach is that it leverages quantum computing’s natural ability to handle the exponential complexity of many-body quantum systems. While classical DFT methods struggle with large systems due to cubic scaling, our quantum approach promises linear scaling with respect to system size.
Implementation Challenges
Working within hackathon constraints, we had to make some practical compromises. We used Chebyshev polynomial approximations to simulate the QSVT behavior classically, since we didn’t have access to actual quantum hardware. We also focused on relatively small system sizes to keep computation tractable during the event.
The trickiest part was getting the self-consistent field loop to converge reliably with the polynomial approximations. We ended up implementing both a full coordinate method (updating all density components) and a randomized block coordinate method (updating only selected components) to speed up convergence.
Results
We successfully demonstrated conductivity predictions for different copper-graphene configurations, showing how the material’s electronic properties change with varying graphene content and positioning. While our results were proof-of-concept level, they showed the potential for quantum-enhanced materials discovery.
Presentation
Technologies Used
- Quantum Computing
- Density Functional Theory
- QSVT
- Materials Science
- Python